Chris Bao's Blog

Table of Contents

First I have to admit that memory management is a big( and important) topic in operating system. This post can’t cover everything related to it.

In this post, I want to share something interesting I learned about stack memory management. Especially understand how the stack frame of function call works, which’s the most important part of stack memory. I will explain the mechanism in detail with examples and diagrams.

Briefly speaking, the contents of this post is:

• Memory layout of a process
• Stack memory contents
• CPU register related to stack memory management
• Stack frame of function call and return mechanism

To understand the concepts and machanisms deeply, a few assembly code will be shown in this post, you don’t have to know assembly lauguage as an expert for reading this post, I will add comments for these assembly codes to make explain what’s their functionalities.

Stack Memory Management Basic

Memory Layout of Process

Before we talk about Stack memory management, it’s necessary to understand memory layout of a process.

When you create a program, it is just some Bytes of data which is stored in the disk. When a program executes then it starts loading into memory and become a live entity. In a more specify way, some memory (virtual memory) is allocated to each process in execution for its usage by operating system. The memory assigned to a process is called process’s virtual address space( short for VAS). And memory layout use diagrams to help you understand the concept of process virtual address space easily.

There are some awesome posts on the internet about memory layout. And the most two critical sections are: Stack and Heap. Simply speaking, Stack is the memory area which is used by each process to store the local variables, passed arguments and other information when a function is called. This is the topic of this post, you’ll know more detailed in the following sections. While Heap segment is the one which is used for dynamic memory allocation, this is another more complex topic out of this post’s scope.

Stack Memory Basics

Stack Memory is just memory region in each process’s virtual address space where stack data structure (Last in, first out) is used to store the data. As we mentioned above, when a new function call is invoked, then a frame of data is pushed to stack memory and when the function call returns then the frame is removed from the stack memory. This is Stack Frame which represent a function call and its argument data. And every function has its own stack frame.

Let’s say in your program there are multiple functions call each other in order. For example, main() -> f1() -> f2() -> f3(), main function calls function one f1(), then function one calls function two f2(), finally function two calls function three f3(). So based on the Last in first out rule, the stack memory will be like as below:

Note: the top of the stack is the bottom part of the image. Don’t feel confused for that.

Stack memory contents

After understand stack frames, now let’s dive deep into each stack frame to discover its contents.

Each stack frame contains 4 parts:

• Parameter passed to the callee function
• Return address of the caller function
• Base pointer
• Local variables of the callee function

Caller and callee is very easy to understand. Let’s say main() -> f1(), then caller function is main() while callee function is f1(). Right?

For the above 4 four parts, there are something need to emphasis. Firstly the size of return address of the caller function is fixed, for example, in 32 bits system the size is 4B. And Base pointer size is fixed as well, it’s also 4B in a 32 bits system. This fixed size is important, you’ll see the reason in following sections.

Next, in the above diagram you see two kinds of pointers: base pointer and stack pointer. Let’s check them one by one.

Stack pointer: pointer to the top of the stack. When stack adds or removes data then stack pointer will change correspondingly. Stack pointer is straight forward and not difficult to understand, right?
Base pointer: is also called frame pointer which points to the current active frame. And the current active frame is the topmost frame of the stack.

The base pointer is conventionlly used to mark the start of a function’s stack frame, and the area of the stack managed by that function. As we mentioned above, since the size of return address and base pointer is fixed, so based on the address of base pointer you can get all the data in that stack frame. Local variables can be accessed with positive offset and passed parameters can be got with negative offset. That’s the reason why it is called base pointer. Great design, right?

The other thing need to discuss is what’t the content of base pointer part in each stack frame? In the above diagram you see that a 4 bytes data is pushed into the stack, we call it base pointer. But what’s the data? In fact, base pointer is designed to store the caller's base pointer address. This is also a smart design to make function return works well. We’ll discuss more about it later.

CPU register

To understand stack memory management, you’ll need to know 3 interesting CPU register:

• eip: Instruction pointer register which stores the address of the next instruction to be run.
• esp: Stack pointer register which stores the address of the top of the stack at any time.
• ebp: Base pointer register which stores base pointer address of callee’s stack frame. And the content at this address is the caller’s base pointer value (we already mentioned this point above).

Until now, you see all the necessary stuff: stack frame, stack frame content and CPU registers. Let’s see how they play together to make stack frames of function call and return works. You’ll see how this simple but beautiful design realizes such a complex task.

Mechanism of function call and return

In this section, you’ll understand how function call and return works by reading a few assembly codes (which are not difficult to understand).

function call

Step one: as you already see in the above diagram the first part of each stack frame is the passed parameters to the callee. So all the arguments are pushed on the stack as the following codes shows:

1
2

push arg2;
push arg1;

push is the assembly instruction to push data onto the stack. And usually the arguments are pushed to the stack in the reverse order that they’re declared in function.

Step two: the second part is the Return address of the caller fn, so we need to push the address of next instruction in caller function as Return address in callee’s stack frame. As we introduced in the last section, the address of next instruction will be stored in EIP register, right? The assembly code goes as following:

1

push eip;

Step three: upon entrying to the callee function, the old EBP value (the caller function’s base pointer address) is pushed onto the stack and then EBP is set to the value of ESP. Then the ESP is decremented (since the stack grows downward in stack memory) to allocate space for the local variables. And the codes goes as following:

1
2

push ebp;
mov ebp esp;

mov - the mov instruction copies the data item referred to by its second operand into the location referred to by its first operand.

So mov %ebp %esp just means set EBP a new value of ESP. Please note that, ESP value changes when data is pushed or popped onto/from the stack. But it’s always points to the top of the stack. Before this mov %ebp %esp instruction, ESP is pointing to the address just after the return address of the caller, and it should be the address of callee’s base pointer and just what EBP should store, this instruction makes sense, right?

From that on, during the execution of the callee function, the passed arguments to the function are located at the positive offsets from EBP, and the local variables are located at the negative offsets from EBP, you already see this conclusion above.

Inside a function, the stack would look like this:

1
2
3
4
5
6

| <argument 2>       |
| <argument 1>       |
| <return address>   |
| <old ebp>          | <= %ebp
| <local var 1>      |
| <local var 2>      | <= %esp

function return

Step one: upon exit from the callee function, all the function has to do is set ESP to the value of EBP. In this way can simply deallocates/releases the local variables from the stack. And then it can also expose callee’s base pointer on the top of the stack for next step operation.

1

mov esp, ebp;

This instruction is restoring the saved value of ESP upon entering the function, at that point what we did is mov ebp esp. Smart design, right?

Step two: since ESP already reset to the address of base pointer, next step we can simply pop the old EBP value from the top of stack as following:

1

pop ebp;

pop instruction retrieves the topmost value from the stack and puts the value into the second operand, in this case is EBP. Remember the callee function’s base pointer stores the caller function’s base pointer, so this simple pop ebp instruction realize EBP register restore perfactly. Great design, right?

Step three: next is straight forward, we need to pop the caller function return address to EIP.

1

pop eip;

Similar to step two, right? Now the system knows the next instruction (pointing to the return address in the caller function) need to run. The execution context is giving back to the caller function.

Upon returning back to the caller function, it can then increase ESP register again to remove the passed function arguments it pushed onto the stack. At this point, the stack frames becomes the same as it was in prior to invoking the callee function.

Why develop in Docker container?

Docker is the hottest technology to deploy and run the software. The key benefit of Docker is that it allows users to package an application with all of its dependencies into a standardized unit for software development. Compared with virtual machines, containers do not have high overhead and hence enable more efficient usage of the underlying system and resources.

Besides deploying and running applications, Docker containers can also make your local development work easier, especially when you need to set up a specific environment with many dependencies.

In my case, I have a project which is a C++ application running on the Linux platform. But on personal machines I’m running macOS and Windows systems, I didn’t install Linux platform on my computer. Before I start working on this project, I need to fix the platform/environment issue.

The first idea is, of course, using virtual-machines with VirtualBox and install the Linux system in it. This process will be time-consuming and tedious. So I decided to use Docker container to speed up the environment configuration step.

I will share the experience step by step. The whole process is lightweight and quick, also can practice your Docker related skills.

Create the Docker container

To build a Docker image, we need a Dockerfile, which is a text document(without a file extension) that contains the instructions to set up an environment for a Docker container. The Docker official site is the best place to understand those fundamental and important knowledge.

In my case the basic Dockerfile goes as following:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Download base image ubuntu 20.04
FROM ubuntu:20.04

# Disable Prompt During Packages Installation
ARG DEBIAN_FRONTEND=noninteractive

# Update Ubuntu Software repository
RUN apt-get update && apt-get install -y \
    make \
    cmake \
    g++ \
    libncurses5-dev \
    libncursesw5-dev \
&& rm -rf /var/lib/apt/lists/*

CMD ["bash"]

FROM : the first part is the FROM command, which tells us what image to base this off of (as we know, Docker is following a multi-layer structure). In my case, it’s using the Ubuntu:20.04 image, which again references a Dockerfile to automate the process.

ARG: ARG instruction defines a variable that can be passed at build time to pass environment info. In this case, just to disable the console output during the following Linux package installation process.

RUN: the next set of calls are the RUN commands. This RUN instruction allows you to install your application and packages for it. RUN executes commands in a new layer and creates a new layer by committing the results. Usually, you can find several RUN instructions in a Dockerfile. In this case, I want to install the C++ compiler and build tools (and some other specific dependency packages for development) which is not available in the Ubuntu base image.

CMD: the last instruction CMD allows you to set a default command, which will be executed when you run the container without specifying a command. If Docker container runs with a command, this default one will be ignored.

With this Dockerfile, we can build the image with the next Docker command:

1

docker build -t linux-cpp .

This will build the desired Docker image tagged as linux-cpp. You can list(find) this new image in your system with command docker images:

1
2

REPOSITORY          TAG                 IMAGE ID            CREATED             SIZE
linux-cpp           latest              5463808c4488        8 days ago          320MB

Now you can run the docker container with the newly build linux-cpp image:

1

docker run -it --name cpp-dev --rm linux-cpp

Mount source code into container

Follow the above steps, you can have a running Docker container with C++ development dependencies in Linux environment.

Next, you can directly start your C++ program inside the container, then build and run your code.

But if you just put your program inside the container, you will have a high risk to lose your code when the container is deleted.

The better way is placing your program source code on your local machine and sync the codes into the container as you program. This is where mount can help you. Mount and Volume is an important topic for Docker, you can find some posts for deeper introduction.

In my case, I can realize my target with the following command:

1

docker run -it --name cpp-dev  --rm  -v ${PWD}:/develop  linux-cpp

the key and interesting part is: -v ${PWD}:/develop, this will mount the current directory of the host machine into the develop directory inside the container. If develop directory is not there, Docker will make it for you.

Note: the current directory pwd command’s usage has some variants based on your host machine. The above command works for the Powershell of Windows, if you are using git bash on Windows, please try:

1

-v /$(pwd):/develop

For Mac users, try the following:

1

-v $(pwd):/develop

Now you can happily code your program in your familiar host machine, save the code change and sync them into the container. Then build and run your code inside the container with every dependency it needs.

Background

Selector is an essential part of the entire NgRx state management system, which is much more complicated than the action and reducer part based on my learning and development experience. Sometimes I feel it is like a black box, which hides many excellent designs and techniques. I spend some time and dig into the source code of NgRx to take a look at the internals of the black box. This post (and later posts) will share some interesting points I found during the process.

When using NgRx, developers always do something like this:

1
2
3
4

export const animalListState: MemoizedSelector<State, Animal[]> = createSelector(
  rootState,
  (state: RootState): AnimalListState => state.animalList
);

createSelector method return a selector function, which can be passed into the store.select() method to get the desired state out of the store.

By default, the type of the returned function from createSelector is MemoizedSelector<State, Result>. Have you ever notice that? This post will introduce what it is and how it works.

What is memoization?

Memoization is a general concept in computer science. Wikipedia explains it as follows:

In computing, memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

You can find many articles online for explaining memoization with code examples. Simply speaking, a hash map is used for the cached result. Technically it’s not difficult at all.

Memoization is a great optimization solution of pure function. Generally speaking, A pure function is a function where the return value is only determined by its input values, without side effects.

As you may know, Selector is a pure function. memoizedSelector is just a normal selector function with memoization optimization. Next, let’s see how it works in the design of the NgRx library.

Source code of memoizedSelector

In the source code of NgRx, you can find the selector related code in the path of platform/modules/store/src/selector.ts.

selector.ts file is roughly 700 lines, which hold all the functionalities of it. There are many interesting points inside this module, which I can share in another article, but this post focus on memoization. So I pick up all the necessary code and put it as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

export type AnyFn = (...args: any[]) => any;

export type ComparatorFn = (a: any, b: any) => boolean;

export type MemoizedProjection = {
    memoized: AnyFn;
    reset: () => void;
    setResult: (result?: any) => void;
};

export function isEqualCheck(a: any, b: any): boolean {
    return a === b;
};

function isArgumentsChanged(
    args: IArguments,
    lastArguments:IArguments,
    comparator: ComparatorFn
) {
    for (let i = 0; i < args.length ; i++) {
        if (!comparator(args[i], lastArguments[i])) {
            return true;
        }
    }
    return false;
}

export function defaultMemoize(
    projectionFn: AnyFn,
    isArgumentsEuqal = isEqualCheck,
    isResultEqual = isEqualCheck
): MemoizedProjection {
    let lastArguments: null | IArguments = null;
    let lastResult: any = null;
    let overrideResult: any;

    function reset() {
        lastArguments = null;
        lastResult = null;
    }

    function setResult(result: any = undefined) {
        overrideResult = result;
    }

    function memoized(): any {
        if (overrideResult !== undefined) {
            return overrideResult;
        } 
        if (!lastArguments) {
            lastResult = projectionFn.apply(null, arguments as any);
            lastArguments = arguments;
            return lastResult;
        }

        if (!isArgumentsChanged(arguments, lastArguments, isArgumentsEuqal)) {
            return lastResult;
        }

        const newResult = projectionFn.apply(null, arguments as any);
        lastArguments = arguments;

        if (isResultEqual(lastResult, newResult)) {
            return lastResult;
        }

        lastResult = newResult;
        return newResult;
    }
    return { memoized, reset, setResult};
}

There are many interesting Typescript stuff in the above code block. But for memoization, you can focus on the method defaultMemoize. In the following section, I will show you how it can make your program run faster.

Explore the memoizedSelector method

To show how memoization works, I create a simple method slowFunction as following, to simulate that a method running very slowly:

1
2
3
4
5
6
7
8
9
10

export function slowFunction(val: number): number {
    const pre = new Date();
    while (true) {
        const now = new Date();
        if (now.valueOf() - pre.valueOf() > 2000) {
            break;
        }
    }
    return val;
}

And then test it with the following scripts:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import { defaultMemoize } from "./memoizedSelector";
import { slowFunction } from "./slowFunction";

// run slowFunction without memoization
console.log("First call of slowFunction(2)");
let pre = new Date();
slowFunction(2);
console.log("It takes" + ((new Date()).valueOf() - pre.valueOf())/1000 +  "seconds \n");
console.log("Second call of slowFunction(2)");
pre = new Date();
slowFunction(2);
console.log("It takes" + ((new Date()).valueOf() - pre.valueOf())/1000 +  "seconds \n");

// run slowFunction with memoization

const fastFunction = defaultMemoize(slowFunction);
console.log("First call of fastFunction(2)");
pre = new Date();
fastFunction.memoized(2);
console.log("It takes" + ((new Date()).valueOf() - pre.valueOf())/1000 +  "seconds \n");
console.log("Second call of fastFunction(2)");
pre = new Date();
fastFunction.memoized(2);
console.log("It takes" + ((new Date()).valueOf() - pre.valueOf())/1000 +  "seconds \n");

The output goes as folllowing:

1
2
3
4
5
6
7
8
9
10
11
12

$ ts-node index.ts
First call of slowFunction(2)
It takes2.001seconds

Second call of slowFunction(2)
It takes2.001seconds

First call of fastFunction(2)
It takes2.002seconds

Second call of fastFunction(2)
It takes0.001seconds

Compared with the original slowFunction method, the memoized method fastFunction can directly output the result for the same input. That’s the power of memoization, hope you can master it.

What’s Marble Testing

RxJS is a powerful tool to handle various asynchronous tasks. Sometime RxJS observables are hard to test. In the community, there is one particular unit testing solution for RxJS observables called marble testing.

For marble testing, you can refer to these articles. They all do an excellent job of introducing what it is.

A real case to show Marble Testing’s power

Recently in my development work, I came across a case where I used marble testing properly to solve the issue.

The background is for my application in the root index.html file, there is one third-party javascript library/SDK. For some business reasons, after the third-party library is loaded, we bind some value to the global window object.

1
2
3

window.onSecretLibraryLoad = (res) => {
  window.SecretLibrary = res; 
};

Before the loaded event is triggered, the window.SecretLibary was undefiend. After the event is triggered, it will be assigned some value.

This global value is vital for my application since one of the UI components depends on it to determine to show or hide.

Since the script was loaded with async flag for performance consideration, this component needs to check the window.SecretLibrary value repeatedly.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

export class UIComponent implements OnInit {
    public isSecretLibraryReady$: Observable<boolean>;
    public ngOnInit(): void {
        this.isSecretLibraryReady$ = this.getSecretLibraryLoadStatus();
    }

    public getSecretLibraryLoadStatus(): Observable<boolean> {
        return timer(0, 500).pipe(
            map((t) => ({
                currentTimeTick: t,
                isReady: Boolean((window as any).SecretLibrary)
            })),
            takeWhile(
                (val) => !val.isReady && val.currentTimeTick <= 30000/500,
                true
            ),
            pluck("isReady")
        );
    }
}

The interesting part comes from the getSecretLibraryLoadStatus function. It utilizes the timer, map, takeWhile, and pluck operators of RxJS library to realize the repeatedly status checking and updating purpose.

RxJS operator is not this article’s topic, so I will not dig deep into it. Just add one comment for the takeWhile part, which seems a little hard to understand at the first look. It defines two conditions to stop the observable: first case is the window.SecretLibrary value is not undefined, which means the script is loaded; the second case is it reaches the maximum time limit (30 seconds).

How to test it: marble testing

Traditionally we use subscribe and assert pattern to test RxJS observables. But for the case, as mentioned above: time-based observables, the traditional solution can’t handle it well. We can’t wait 30 seconds when we run the unit tests during local development or in CI pipeline. That’s unacceptable.

Marble testing can fix this issue correctly by the concept of virtual time. For what is virtual time, you can refer to these great articles. I will not discuss it at a detailed level in this post. Simply speaking, virtual time empowers us to test asynchronous RxJS observable synchronously. In virtual time asynchronous functions like setTimeout and setInterval will use fake time instead of actual time. And the magic comes from the TestScheduler of RxJS.

The marble testing solution as following:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

describe("UIComponent", () => {
  let component: UIComponent;
  let fixture: ComponentFixture<UIComponent>;
  let scheduler: TestScheduler;

  beforeEach(async(() => {
    TestBed.configureTestingModule({
      declarations: [UIComponent],
    }).compileComponents();
  }));

  beforeEach(() => {
    fixture = TestBed.createComponent(UIComponent);
    component = fixture.componentInstance;
    scheduler = new TestScheduler((actual, expected) => expect(actual).toEqual(expected));
    (window as any).SecretLibrary = undefined;
  });

  it("getSecretLibraryLoadStatus method should return a boolean observable stream, for script load success case", () => {
    scheduler.run(({ expectObservable }) => {
      timer(2 * 1000).subscribe(() => {
        (window as any).SecretLibrary = "SecretLibrary";
      });
      // tricky point about marble test: a, b, c these placeholders account 1 frame of virtual time
      expectObservable(component.getSecretLibraryLoadStatus()).toBe(
        "a 499ms b 499ms c 499ms d 499ms (e|)",
        {
          a: false,
          b: false,
          c: false,
          d: false,
          e: true
        }
      );
    });
  });
});

Let me emphasize several key points to understand the above testing case. getSecretLibraryLoadStatus will repeatedly check the status of window.SecretLibrary every 500 milliseconds and return a boolean value stream.

I manually set the window.SecretLibrary value after 2 seconds by calling this:

1
2
3

timer(2 * 1000).subscribe(() => {
  (window as any).SecretLibrary = "SecretLibrary";
});

So Let’s imagine what the result should be: the first four emit value will be false, and the last value is true. That’s the expected observable.

But please notice that scheduler.run, everything run inside the callback will use virtual time. So we didn’t wait 2 seconds for the timer operator. Instead, it runs synchronously.

The second point needs to notice is the syntax of the marble string a 499ms b 499ms c 499ms d 499ms (e|). Yes, it looks a little wired, but be careful that’s the correct way to represent marble. The alphanumeric values represent an actual emitted value, which advances time one virtual frame.

Here I only show the case where the third-party script load successfully. Of course, to have full testing coverage, we need to consider the negative case where the script failed to load. You can figure it out.

Summary

In this post, I didn’t go into the detailed syntax of marble testing. I think the reader can find the related document easily. I record a real usage case in the development where marble testing can show its power to handle async observables.

Part 2

Circular List

Judge a linked list is circular or not

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function circular(list) {
  let slow = list.getFirst();
  let fast = list.getFirst();

  while (fast.next && fast.next.next) {
    slow = slow.next;
    fast = fast.next.next;

    if (slow === fast) {
      return true;
    }
  }

  return false;
}

Tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

class Node {
  constructor(data) {
    this.data = data;
    this.children = [];
  }

  add(data) {
    this.children.push(new Node(data));
  }

  remove(data) {
    this.children = this.children.filter(node => {
      return node.data !== data;
    });
  }
}

class Tree {
  constructor() {
    this.root = null;
  }
  // 广度优先
  traverseBF(fn) {
    // 初始化一个数组
    const arr = [this.root];
    // 循环判断
    while (arr.length) {
      // 取得头部的元素
      const node = arr.shift();
      // 把头部元素的children push到array里
      arr.push(...node.children);
      fn(node);
    }
  }
  // 深度优先
  traverseDF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();

      arr.unshift(...node.children);
      fn(node);
    }
  }
}

module.exports = { Tree, Node };

Tree level width

1
2
3
4
5
6
7
8
9
10
11
12

Given the root node of a tree, return
an array where each element is the width
of the tree at each level.
--- Example
Given:
    0
  / |  \
1   2   3
|       |
4       5
Answer: [1, 3, 2]

solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function levelWidth(root) {
  const arr = [root, 's'];
  const counters = [0];

  while (arr.length > 1) {
    const node = arr.shift();

    if (node === 's') {
      counters.push(0);
      arr.push('s');
    } else {
      arr.push(...node.children);
      counters[counters.length - 1]++;
    }
  }

  return counters;
}

Events

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

// --- Directions
// Create an 'eventing' library out of the
// Events class.  The Events class should
// have methods 'on', 'trigger', and 'off'.

class Events {
  constructor() {
    this.events = {};
  }

  // Register an event handler
  on(eventName, callback) {
    if (this.events[eventName]) {
      this.events[eventName].push(callback);
    } else {
      this.events[eventName] = [callback];
    }
  }

  // Trigger all callbacks associated
  // with a given eventName
  trigger(eventName) {
    if (this.events[eventName]) {
      for (let cb of this.events[eventName]) {
        cb();
      }
    }
  }

  // Remove all event handlers associated
  // with the given eventName
  off(eventName) {
    delete this.events[eventName];
  }
}

Binary Search Tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

// 1) Implement the Node class to create
// a binary search tree.  The constructor
// should initialize values 'data', 'left',
// and 'right'.
// 2) Implement the 'insert' method for the
// Node class.  Insert should accept an argument
// 'data', then create an insert a new node
// at the appropriate location in the tree.
// 3) Implement the 'contains' method for the Node
// class.  Contains should accept a 'data' argument
// and return the Node in the tree with the same value.
// If the value isn't in the tree return null.

class Node {
  constructor(data) {
    // 每个node三个属性
    this.data = data;
    this.left = null;
    this.right = null;
  }

  insert(data) {
    if (data < this.data && this.left) {
      //对left子节点的递归insert
      this.left.insert(data);
    } else if (data < this.data) {
      // 赋值给left子节点
      this.left = new Node(data);
    } else if (data > this.data && this.right) {
      //对right子节点的递归insert
      this.right.insert(data);
    } else if (data > this.data) {
      // 赋值给right子节点
      this.right = new Node(data);
    }
  }

  contains(data) {
    if (this.data === data) {
      return this;
    }

    if (this.data < data && this.right) {
      // right子节点的contains操作
      return this.right.contains(data);
    } else if (this.data > data && this.left) {
      // left子节点的contains操作
      return this.left.contains(data);
    }

    return null;
  }
}

Validate the Binary Search Tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

function validate(node, min = null, max = null) {
  if (max !== null && node.data > max) {
    return false;
  }

  if (min !== null && node.data < min) {
    return false;
  }

  if (node.left && !validate(node.left, min, node.data)) {
    return false;
  }

  if (node.right && !validate(node.right, node.data, max)) {
    return false;
  }

  return true;
}

BubbleSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function bubbleSort(arr) {
  // Implement bubblesort
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < (arr.length - i - 1); j++) {
      if (arr[j] > arr[j+1]) {
        const lesser = arr[j+1];
        arr[j+1] = arr[j];
        arr[j] = lesser;
      }
    }
  }

  // return the sorted array
  return arr;
}

Selection Sort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let indexOfMin = i;

    for (let j = i+1; j <arr.length; j++) {
      if (arr[j] < arr[indexOfMin]) {
        indexOfMin = j;
      }
    }

    if (indexOfMin !== i) {
      let lesser = arr[indexOfMin];
      arr[indexOfMin] = arr[i];
      arr[i] = lesser;
    }
  }

  return arr;
}

Merge Sort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

function mergeSort(arr) {
  if (arr.length === 1) {
    return arr;
  }

  const center = Math.floor(arr.length / 2);
  const left = arr.slice(0, center);
  const right = arr.slice(center);
  // 神奇的递归
  return merge(mergeSort(left), mergeSort(right));
}

// 辅助函数merge，能够把两个已经排序的left和right数组，整合排序为一个array
function merge(left, right) {
  const results = [];

  while (left.length && right.length) {
    if (left[0] < right[0]) {
      results.push(left.shift());
    } else {
      results.push(right.shift());
    }
  }
  // 到这行的时候，left和right，至少有一个是空的了，所以不用纠结left和right的前后位置了。
  return [...results, ...left, ...right];
}

binary Gap

A binary gap within a positive integer N is any maximal sequence of consecutive zeros that is surrounded by ones at both ends in the binary representation of N.

For example, number 9 has binary representation 1001 and contains a binary gap of length 2. The number 529 has binary representation 1000010001 and contains two binary gaps: one of length 4 and one of length 3. The number 20 has binary representation 10100 and contains one binary gap of length 1. The number 15 has binary representation 1111 and has no binary gaps. The number 32 has binary representation 100000 and has no binary gaps.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function binaryGap(num) {
  let str = num.toString(2).split('')
  console.log(str)
  let counter = 0;
  let max = 0;
  str.forEach((char) =>  {
    if (char === '0') {
      counter ++;
    } else {
      if (counter > max) {
        max = counter;
      }
      counter = 0;
    }
    // console.log(counter)
  });
  return max;
}

Bug and Sell Stock

You will be given a list of stock prices for a given day and your goal is to return the maximum profit that could have been made by buying a stock at the given price and then selling the stock later on. For example if the input is: [45, 24, 35, 31, 40, 38, 11] then your program should return 16 because if you bought the stock at $24 and sold it at $40, a profit of $16 was made and this is the largest profit that could be made. If no profit could have been made, return -1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

function getMaxProfit(arr) {
  var minIdx = 0;
    var maxIdx = 1;
    var currMin = 0;
    var maxProfit = 0;

    if(arr.length < 2) {
        throw new Error("Need atleast two time periods to be profitable!");
    }

    for(var i = 1; i < arr.length; i++) {

        // new current min.
        if(arr[i] < arr[currMin]) {
          currMin = i;
        }

        // new best profit
        if(arr[maxIdx] - arr[minIdx] < arr[i] - arr[currMin]) {
                maxIdx = i;
              minIdx = currMin;
        }

    }

    maxProfit  = arr[maxIdx] - arr[minIdx];
    return maxProfit;
}

The Coding Interview Bootcamp: Data structure and algorithm.

Part 1

String Reverse

1
2
3

function reverse(str) {
  return str.split('').reduce((rev, char) => char + rev, '');
}

Paldinromes

1
2
3
4
5

function palindrome(str) {
  return str.split('').every((char, i) => {
    return char === str[str.length - i - 1];
  });
}

another way is based on recursive method:

1
2
3
4
5
6
7
8
9
10
11

function palindromeRecursive(str) {
  if (str.length <= 1) {
    return true;
  } else {
    if (str[0] !== str[str.length - 1]) {
      return false;
    } else {
      return palindromeRecursive(str.substring(1, str.length - 1))
    }
  }
}

Longest Paldinromes substring

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

function longestPalin(str) {
  str = treatStr(str);
  console.log(str)
  let max =  0;
  for (let i  = 1; i < str.length - 1; i++) {
    let radius = Math.min (i, str.length - i - 1);
    console.log(radius)
    let currentMax = getMaxSubLength(str, i, radius);
    if (max < currentMax) {
      max = currentMax + 1;
    }
  }
  return max;
}

function getMaxSubLength(str, i, radius) {
  let max = 0;
  for (let j = 0; j <= radius; j++) {
    if (str[i - j] === str[i + j]) {
      max = j;
    } else {
      break;
    }
  }
  return max;
}

function treatStr(str) {
  let rtn = '';
  for (let i = 0; i < str.length; i++) {
    if (i === str.length - 1) {
      rtn = rtn + str[i];
    } else  {
      rtn = rtn + str[i] + '#';
    }

  }
  return rtn;
}

Integer Reversal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

// --- Directions
// Given an integer, return an integer that is the reverse
// ordering of numbers.
// --- Examples
//   reverseInt(15) === 51
//   reverseInt(981) === 189
//   reverseInt(500) === 5
//   reverseInt(-15) === -51
//   reverseInt(-90) === -9

function reverseInt(n) {
  const reversed = n
    .toString()
    .split('')
    .reverse()
    .join('');

  return parseInt(reversed) * Math.sign(n);
}

Anagrams

method1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

function anagrams(stringA, stringB) {
  const aCharMap = buildCharMap(stringA);
  const bCharMap = buildCharMap(stringB);

  if (Object.keys(aCharMap).length !== Object.keys(bCharMap).length) {
    return false;
  }

  for (let char in aCharMap) {
    if (aCharMap[char] !== bCharMap[char]) {
      return false;
    }
  }

  return true;
}

function buildCharMap(str) {
  const charMap = {};

  for (let char of str.replace(/[^\w]/g, '').toLowerCase()) {
    charMap[char] = charMap[char] + 1 || 1;
  }

  return charMap;
}

method2

1
2
3
4
5
6
7
8
9
10
11
12

function anagrams(stringA, stringB) {
  return cleanString(stringA) === cleanString(stringB);
}

function cleanString(str) {
  return str
    .replace(/[^\w]/g, '')
    .toLowerCase()
    .split('')
    .sort()
    .join('');
}

Printing Steps

The effect we need is as following:

1
2
3
4
5
6
7
8
9
10
11
12
13

--- Examples
  steps(2)
      '# '
      '##'
  steps(3)
      '#  '
      '## '
      '###'
  steps(4)
      '#   '
      '##  '
      '### '
      '####'

solution based on recursive methods

1
2
3
4
5
6
7
8
9
10
11
12
13

function steps(n, row = 0, stair = '') {
  if (n === row) {
    return;
  }

  if (n === stair.length) {
    console.log(stair);
    return steps(n, row + 1);
  }

  const add = stair.length <= row ? '#' : ' ';
  steps(n, row, stair + add);
}

Enter the Matrix Spiral

The requirement goes as following:

1
2
3
4
5
6
7
8
9
10
11
12
13

--- Examples
  matrix(2)
    [[undefined, undefined],
    [undefined, undefined]]
  matrix(3)
    [[1, 2, 3],
    [8, 9, 4],
    [7, 6, 5]]
 matrix(4)
    [[1,   2,  3, 4],
    [12, 13, 14, 5],
    [11, 16, 15, 6],
    [10,  9,  8, 7]]

solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

function matrix(n) {
  const results = [];

  for (let i = 0; i < n; i++) {
    results.push([]);
  }

  let counter = 1;
  let startColumn = 0;
  let endColumn = n - 1;
  let startRow = 0;
  let endRow = n - 1;
  while (startColumn <= endColumn && startRow <= endRow) {
    // Top row
    for (let i = startColumn; i <= endColumn; i++) {
      results[startRow][i] = counter;
      counter++;
    }
    startRow++;

    // Right column
    for (let i = startRow; i <= endRow; i++) {
      results[i][endColumn] = counter;
      counter++;
    }
    endColumn--;

    // Bottom row
    for (let i = endColumn; i >= startColumn; i--) {
      results[endRow][i] = counter;
      counter++;
    }
    endRow--;

    // start column
    for (let i = endRow; i >= startRow; i--) {
      results[i][startColumn] = counter;
      counter++;
    }
    startColumn++;
  }

  return results;
}

Fibonacci

solution based on memoization and recursive.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

function memoize(fn) {
  const cache = {};
  return function(...args) {
    if (cache[args]) {
      return cache[args];
    }

    const result = fn.apply(this, args);
    cache[args] = result;

    return result;
  };
}

function slowFib(n) {
  if (n < 2) {
    return n;
  }

  return fib(n - 1) + fib(n - 2);
}

const fib = memoize(slowFib);

The most simplified method goes as following:

1
2
3
4
5
6
7
8
9
10
11
12

function memoize(fn) {
  const cache = {};
  return function(n) {
    if(cache[n]) {
      return cache[n];
    }
    const result = fn(n);
    cache[n] = result;

    return result;
  }
}

Make it more abstract like below:

1
2
3
4
5
6
7
8
9
10
11
12
13

function memoize(fn) {
  const cache = {};
  return function(...args) {
    if (cache[args]) {
      return cache[args];
    }

    const result = fn.apply(this, args);
    cache[args] = result;

    return result;
  };
}

Queue and Stack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Queue {
  constructor() {
    this.data = [];
  }

  add(record) {
    this.data.unshift(record);
  }

  remove() {
    return this.data.pop();
  }
}

class Stack {
  constructor() {
    this.data = [];
  }

  push(record) {
    this.data.push(record);
  }

  pop() {
    return this.data.pop();
  }

  peek() {
    return this.data[this.data.length - 1];
  }
}

Two Become One

Implement a Queue data structure using two stacks

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

const Stack = require('./stack');

class Queue {
  constructor() {
    this.first = new Stack();
    this.second = new Stack();
  }

  add(record) {
    this.first.push(record);
  }

  remove() {
    while (this.first.peek()) {
      this.second.push(this.first.pop());
    }

    const record = this.second.pop();

    while (this.second.peek()) {
      this.first.push(this.second.pop());
    }

    return record;
  }

  peek() {
    while (this.first.peek()) {
      this.second.push(this.first.pop());
    }

    const record = this.second.peek();

    while (this.second.peek()) {
      this.first.push(this.second.pop());
    }

    return record;
  }
}

Linked List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154

class Node {
  constructor(data, next = null) {
    this.data = data;
    this.next = next;
  }
}

class LinkedList {
  constructor() {
    this.head = null;
  }

  insertFirst(data) {
    this.head = new Node(data, this.head);
  }

  size() {
    let counter = 0;
    let node = this.head;

    while (node) {
      counter++;
      node = node.next;
    }

    return counter;
  }

  getFirst() {
    return this.head;
  }

  getLast() {
    if (!this.head) {
      return null;
    }

    let node = this.head;
    while (node) {
      if (!node.next) {
        return node;
      }
      node = node.next;
    }
  }

  clear() {
    this.head = null;
  }

  removeFirst() {
    if (!this.head) {
      return;
    }

    this.head = this.head.next;
  }

  removeLast() {
    if (!this.head) {
      return;
    }

    if (!this.head.next) {
      this.head = null;
      return;
    }

    let previous = this.head;
    let node = this.head.next;
    while (node.next) {
      previous = node;
      node = node.next;
    }
    previous.next = null;
  }

  insertLast(data) {
    const last = this.getLast();

    if (last) {
      // There are some existing nodes in our chain
      last.next = new Node(data);
    } else {
      // The chain is empty!
      this.head = new Node(data);
    }
  }

  getAt(index) {
    let counter = 0;
    let node = this.head;
    while (node) {
      if (counter === index) {
        return node;
      }

      counter++;
      node = node.next;
    }
    return null;
  }

  removeAt(index) {
    if (!this.head) {
      return;
    }

    if (index === 0) {
      this.head = this.head.next;
      return;
    }

    const previous = this.getAt(index - 1);
    if (!previous || !previous.next) {
      return;
    }
    previous.next = previous.next.next;
  }

  insertAt(data, index) {
    if (!this.head) {
      this.head = new Node(data);
      return;
    }

    if (index === 0) {
      this.head = new Node(data, this.head);
      return;
    }

    const previous = this.getAt(index - 1) || this.getLast();
    const node = new Node(data, previous.next);
    previous.next = node;
  }

  forEach(fn) {
    let node = this.head;
    let counter = 0;
    while (node) {
      fn(node, counter);
      node = node.next;
      counter++;
    }
  }

  *[Symbol.iterator]() {
    let node = this.head;
    while (node) {
      yield node;
      node = node.next;
    }
  }
}

Find the midpoint of linked list

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

--- Directions
Return the 'middle' node of a linked list.
If the list has an even number of elements, return
the node at the end of the first half of the list.
*Do not* use a counter variable, *do not* retrieve
the size of the list, and only iterate
through the list one time.
--- Example
  const l = new LinkedList();
  l.insertLast('a')
  l.insertLast('b')
  l.insertLast('c')
  midpoint(l); // returns { data: 'b' }

function midpoint(list) {
  let slow = list.getFirst();
  let fast = list.getFirst();

  while (fast.next && fast.next.next) {
    slow = slow.next;
    fast = fast.next.next;
  }

  return slow;
}

Multiply two Big numbers

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

function addbyStr(str1, str2) {
  let len = Math.max(str1.length, str2.length);
  let increase = 0;
  let rtn = '';
  for (let i = 0; i < len; i++) {
    let ope1 = i <= str1.length - 1 ? str1[str1.length - 1 -i] : '0';
    let ope2 = i <= str2.length - 1 ? str2[str2.length - 1 -i] : '0';
    let temp = parseInt(ope1) + parseInt(ope2) + increase;
    if (temp >= 10) {
      increase = 1;
      temp = temp - 10;
    } else {
      increase = 0;
    }
    rtn = temp + rtn;
  }
  return rtn;
}


function addArr(arr) {
  let result = arr.reduce((rtn, each) => {
    return rtn = addbyStr(rtn, each);
  });
  return result;
}

function mutliTwoStr(str1, str2) {
  let rtn = [];
  for (let i = 0; i < str2.length; i++) {
    let count = parseInt(str2[str2.length - 1 - i]);
    let temp = new Array(count).fill(str1)
    let tempResult = addArr(temp)
    tempResult =  tempResult + '0'.repeat(i)
    rtn.push(tempResult)
  }
  return addArr(rtn);
}

Background

In Linux world softwares are delivered in the form of package. As a software engineer wants to work in Linux platform, you’ll run package management commands again and again. So you need to understand what actually happens when you run such commands. In this article, I’ll introduce this topic.

Note that different Linux distros have different package management tool. In this article let’s focus on Ubuntu system and the package management tool is apt.

Software repositories

Nowadays, everybody is familiar with app store, which is one central location. And users can retrieve applications there. In Linux world, software repositories work just like app store. Software repositories are generally made available in the form of mirros, to which your Linux system subscribe.

There are many repository mirrors in the world, you can decide which ones to use. In Ubuntu system, it’s defined in the config file of /etc/apt/sources.list as follows:

The URLs defined in the file are just software repositories.

Package index

The APT package index is essentially a database of available packages from the repositories mentioned above.

In Ubuntu system, the package index files are stored in /var/lib/apt/lists

apt update

Based on the above two points, we can easily understand what happens when we run apt update. It doesn’t update any installed packages, instead it updates the package index files in your local machine by sending new network requests to the software repositories. That’s also the reason why we need to run it before we run apt upgrade or apt install. Because the upgraded version or the newly installed version will depend on the updated package index files. In this way users will get the lastest version of the target package.

apt-cache search

Before you actually install a package, you can run apt-cache search command with the package name to get the list of any matched available packages. This can help you in case that you don’t know the exact package name in advance.

apt-cache command doesn’t send any network request, instead it works based on the package index files in your local machine. How to prove this point? Of course the most direct way is reading the source code. But I want to show you another way to prove it with the tool of strace.

strace is a tool can show you all the invoked system call when you run a command. If our guess about apt-cache search is correct, it should invoke system call to read the files in the package index directory /var/lib/apt/lists, right? Let’s have a look by running this command:

1

strace apt-cache search openvpn 2>&1 | grep open

Not that the 2>&1 part in the preceding command, this is because strace writes all its output to stderr, not stdout. And a pipe redirects stdout, not stderr. So you need to redirect stderr of strace to stdout before piping to grep. The output is very long but contains the following lines:

Same as what we guessed. All right.

apt install

There are many people asking questions on the forums about the secret of apt install like this one. Does apt install download the source code of packages and then build it on your machine? That’s also one of the question came to my mind when I first touched Linux world. My intuition tells me there shouldn’t be compiling and building process involved when I run apt install. Because I think it’s too time consuming.

In fact, apt install is used to install the prebuilt binary package to your machine. Simply speaking, it does two tasks:

• Download the package, a Debian package, to /var/cache/apt/archives
• Extract files from the Debian package and copy them to the specific system location

Because Ubuntu is originated from Debian system, so the package you install on Ubuntu is in fact a Debian package which is an archive file with the name ending .deb. For instance, the openvpn Debian package is as follows:

Then we can use ar x <package_name.deb> command to extract the package, you will find that there are three files inside each Debian package:

• debian-binary – A text file indicating the version of the .deb package format.
• control.tar.gz – A compressed file and it contains md5sums and control directory for building package.
• data.tar.xz – A compressed file and it contains all the files to be installed on your system. This is what we need continue to exmpolre.

Run the following tar command to open this tarball

1

tar -xf data.tar.xz

Note that the tarball contains the following directories:

take a look into the usr directory, you’ll find the prebuild binaries.

Background

After you learn and understand how to write small C programs in Linux (that means you know the syntax of C language and how to compile your programs with gcc), you will want to have some adventures to write more powerful and larger programs. To be a great software engineer, you need this passion to explore, right?

To write a larger program, you can’t build everything from scratch. This means you need to import and use libraries developed by others in your program.

For new developers of Linux C programming, the whole handling of libraries can be a mystery, which requires knowledge about gcc compiler, Linux system, GNU conventions and so on. In this article, I will focus on this topic and piece all these together. After reading this post, I hope you can feel free and confident to add the shared libraries from the open source world to your program.

Note: To illustrate the discussion more clearly, this article is based on this demo github app. And my demo app is forked from Stephan Avenwedde’s original repo. Thanks for that.

The code logic of this demo app is very straightforward, so I will not review the code line by line in this article, which is not the target of this post.

Static library vs Shared library

Generally speaking, there are two types of libraries: Static and Shared.

• static library: is simply a collection of ordinary object files; conventionally, static libraries end with the .a suffix. This collection is created using ar command. For example, in the demo app, we build the static library like this:

1
2
3
4
5
6
7
8
9
10

CFLAGS =-Wall -Werror

libmy_static.a: libmy_static_a.o libmy_static_b.o
	ar -rsv ./lib/static/libmy_static.a libmy_static_a.o libmy_static_b.o

libmy_static_a.o: libmy_static_a.c
	cc -c libmy_static_a.c -o libmy_static_a.o $(CFLAGS)

libmy_static_b.o: libmy_static_b.c
	cc -c libmy_static_b.c -o libmy_static_b.o $(CFLAGS)

In our case, the static library will be installed in the subdirectory ./lib/static and named as libmy_static.a.

When the application links against a static library, the library’s code becomes part of the resulting executable. So you can run the application without any further setting or configuration. That’s the biggest advantage of the static library, and you’ll see how it works in the next section.

Static libraries aren’t used as often as they once were, since shared library has more advantages.

• shared library: end with .so which means shared object. The shared library is loaded into memory when the application starts. If multiple applications use the same shared library, the shared library will be loaded only once. In our demo app, the shared library is built as follows:

1
2
3
4
5

libmy_shared.so: libmy_shared.o
	cc -shared -o ./lib/shared/libmy_shared.so libmy_shared.o

libmy_shared.o: libmy_shared.c
	cc -c -fPIC libmy_shared.c -o libmy_shared.o

The shared library libmy_shared.so is installed inside ./lib/shared subdirectory. Note that the shared library is built with some special options for gcc, like -fPIC and -shared. In detail, you can check the document of gcc.

Naming convention

Generally speaking, the name of shared library follows the pattern: lib + name of library + .so. Of course, version information is very important, but in this article, let’s ignore the version issue.

Link library

After building the libraries, next step you need to import the libraries in your app. For our app, the source code is the file of demo/main.c as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#include <stdio.h>
#include <libmy_shared.h>
#include <libmy_static_a.h>
#include <libmy_static_b.h>

int main(){

    printf("Press Enter to repeat\n\n");
    do{
        int n = getRandInt();
        n = negateIfOdd(n);
        printInteger(&n);

    } while (getchar() == '\n');
   
    return 0;
}

Note that we import three header file of our libraries. The next question is how to build the demo app.

Let’s recall the building process of a C program as follows:

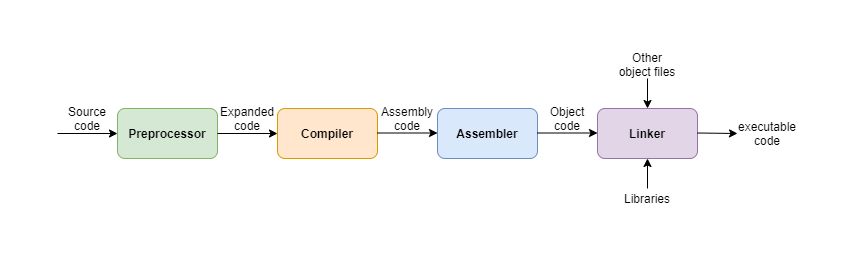
This is a two-step process: compile and link. Firstly, the source code file of main.c will be compiled to an object file, let’s say main.o file. In this step, the critical thing is telling gcc where to find the header file of the libraries. Next, link the main.o object file with our libraries: libmy_static.a and libmy_shared.so. gcc needs to know the name of library it should link and where to find these libraries, right?

These information can be defined by the following three options:

• I: add the include directory for header files,
• l: name of the library
• L: the directory for the library

In our case, the make command to build the demo app is as follows:

1
2
3
4
5
6

LIBS = -L../lib/shared -L../lib/static -lmy_shared -lmy_static -I../

CFLAGS =-Wall -Werror

demo: 
	cc -o my_app main.c $(CFLAGS) $(LIBS)

Since we have two libraries: libmy_static.a and libmy_shared.so, based on the naming convention we mentioned above, the -l option for library name should be my_static and my_shared. We can use two -l options for each library.

For the -L option, we need to provide the directory path where to find the libraries. We can use the path ../lib/shared and ../lib/static relative to the demo’s source code file. Right? And the same rule applies to the -I option for the include header file as well.

Run make demo command, and you can build the demo app with the libraries linked together successfully.

Filesystem placement convention

As I show above, the libraries are placed inside the subdirectory of this project. This is inconvenient for others to import your library. Most open source software tends to follow the GNU standards. The GNU standards recommend installing by default all libraries in /usr/local/lib and all the header files in /usr/local/include when distributing source code. So let’s add one more make command to install the library file and header file to the directory based on the GNU convention:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

INSTALL ?= install
PREFIX ?= /usr/local
LIBDIR = $(PREFIX)/lib
INCLUDEDIR = $(PREFIX)/include

install: library
	$(INSTALL) -D libmy_shared.h $(INCLUDEDIR)/libmy_shared.h
	$(INSTALL) -D libmy_static_a.h $(INCLUDEDIR)/libmy_static_a.h
	$(INSTALL) -D libmy_static_b.h $(INCLUDEDIR)/libmy_static_b.h
	$(INSTALL) -D ./lib/static/libmy_static.a $(LIBDIR)/libmy_static.a
	$(INSTALL) -D ./lib/shared/libmy_shared.so $(LIBDIR)/libmy_shared.so

uninstall:
	rm $(INCLUDEDIR)/libmy_shared.h
	rm $(INCLUDEDIR)/libmy_static_a.h
	rm $(INCLUDEDIR)/libmy_static_b.h
	rm $(LIBDIR)/libmy_static.a
	rm $(LIBDIR)/libmy_shared.so

You can find the similar make command in my open source projects for this purpose.

The benefit is gcc compiler (which is also from GNU and follows the same convention) will look for the libraries by default in these two directories: /usr/local/lib and /usr/local/include. So you don’t need to set -L and -I options. For example, after we run make install command above and install the library into the system directory, you can build the demo app as follows:

1
2
3
4
5
6
7
8

GNULIBS = -lmy_shared -lmy_static

CFLAGS =-Wall -Werror

# you can run this make command after you install 
# the libraries into the default system directory: /usr/local/bin
gnudemo: 
	cc -o my_app main.c $(CFLAGS) $(GNULIBS)

Understand the GNU convention can make your development more easier, right?

Then next step let’s run the demo app by simply calling ./my_app, but you’ll get the following error message:

1

./my_app: error while loading shared libraries: libmy_shared.so: cannot open shared object file: No such file or directroy

What’s happening?

Dynamic linker

When we start up an executable, the Linux kernel automatically runs the dynamic linker (or dynamic loader). This dynamic linker, in turn, finds and loads all other shared libraries used by the program.

In fact, the executable file in Linux system is usually in the format of ELF which abbreviates Executable and Linkable Format. The ELF executable contains linking information, and the dynamic linker just reads that information to load shared libraries.

In Linux system, the dynamic linker is name ld.so

Based on the above error message, we can say that the dynamic linker cannot find the shared library. We can verify this point by running ldd command, which is used to print the shared objects (shared libraries) required by each program or shared object specified on the command line.

Clearly, our shared library libmy_shared.so is not found. We need to take a look how at ld.so works. The best way to find such information is running man command. We can get the following information in the ld.so man document:

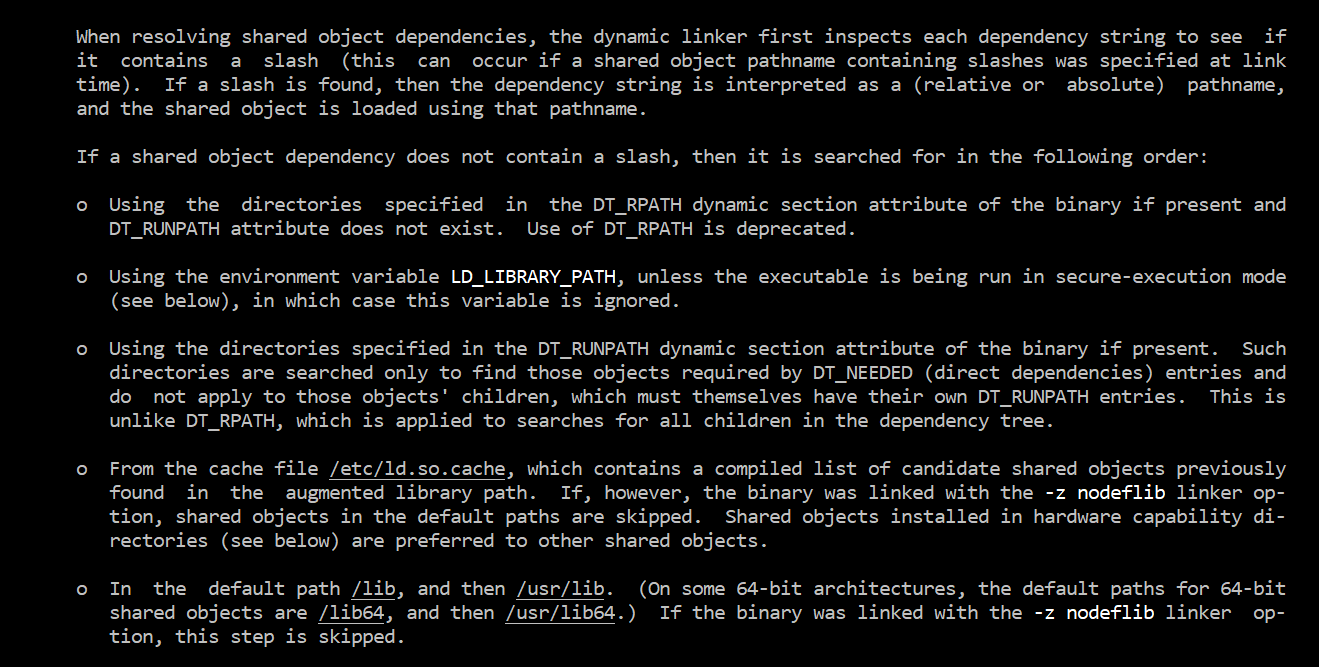
Based on this screenshot, we can solve this issue in three ways:

• install the shared library in the directory: /lib or /usr/lib
• edit the environment variable LD_LIBRARY_PATH by appending the path of directories containing our library
• update the cache file /etc/ld.so.cache

The first two methods can work well based on my test, but personally I recommend to use the third method, which is a more systematic way to register a library.

Register library

To register a new library, we need to use command ldconfig which configures dynamic linker run-time bindings.

How does ldconfig work? It will search .so library files in some specific directories, and the search result will be updated to dynamic linker’s cache file /etc/ld.so.cache.

And one of the directory ldconfig will look at is /etc/ld.so.conf. In our Ubuntu system, it’s in fact a file as follows:

it is expanded to all the .conf files inside ld.so.conf.d, in my case, there is one default file libc.conf as follows:

Note that /usr/local/lib is defined inside the file, then ldconfig will search .so libraries in this directory.

As we mentioned in above section, /usr/local/lib is just the place to install shared library based on GNU convention. Right?

So we can simply run ldconfig command without any option to register a new library (make sure the library is install in that directory):

In the above screenshot, you can see the change before and after running command sudo ldconfig. (ldconfig -p will list the current libraries reading from cache file /etc/ld.so.cache). After registering the library, it is added into the cache file of dynamic linker, right? Let’s verify this again with ldd:

Our new shared library can be found! Then we can run the app successfully as well.

Summary

In this article we discussed several important tools like ld.so, ldd, ldconfig and gcc, which help you build and import shared libraries. Another thing is GNU convention or standard which defines the behavior of these tools.

Background

In the previous articles of this series, we examined how digital signatures and certificates make the TLS handshake process work. Generally speaking, this process is handled by platforms like web browsers. In this article, I want to demystify the process of TLS handshake by manual verification of SSL/TLS certificates step by step.

Certificate chain

In this previous article, we mentioned that the server returns not one, but multiple certificates. These associated certificates form a certificate chain as follows:

The intermediate CA signs the server certificate, and Root CA signs the certificate of the intermediate CA (There can be multiple intermediate CAs). Pay attention to the subject and issuer names of each certificate, and you can notice that one certificate’s issue name is another certificate’s subject name. Certificates can find their CA’s certificate in the chain with this information.

For example, the following openssl command prints the certificate chain of google.com:

1

openssl s_client -showcerts -connect google.com:443

The previous article explained that the chain contains three certificates. Let us extract the google.com server certificate into file google_com.pem and the intermediate CA certificate into file intermediate_ca.pem. These two files are the input data for this manual verification experiment.

Manual verification of SSL/TLS certificates

The entire process can be illustrated as follows:

Let us go through it step by step.

Extract the public key of intermediate CA

Since the certificate of the google.com server is signed with intermediate CA’s private key. The first step is to extract the public key of intermediate CA from its certificate.

1

openssl x509 -in ./intermediate_ca.pem -noout -pubkey > ./intermediate_ca_pub.pem

The content of file intermediate_ca_pub.pem goes as follows:

1
2
3
4
5
6
7
8
9

-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEA9Yjf52KMHjf4N0KQf2yH
0PtlgiX96MtrpP9t6Voj4pn2HOmSA5kTfAkKivpC1l5WJKp6M4Qf0elpu7l07FdM
ZmiTdzdVU/45EE23NLtfJXc3OxeU6jzlndW8w7RD6y6nR++wRBFj2LRBhd1BMEiT
G7+39uBFAiHglkIXz9krZVY0ByYEDaj9fcou7+pIfDdNPwCfg9/vdYQueVdc/Fdu
Gpb//Iyappm+Jdl/liwG9xEqAoCA62MYPFBJh+WKyl8ZK1mWgQCg+1HbyncLC8mW
T+9wScdcbSD9mbS04soud/0t3Au2axMMjBkrF5aYufCL9qAnu7bjjVGPva7Hm7GJ
nQIDAQAB
-----END PUBLIC KEY-----

You can look at the public key in PEM format (which is not readable to humans).

Extract the signature

Next, let us extract the digital signature of the google.com server’s certificate. This task is a little bit complex, and we need several Linux commands to form a data stream pipeline as follows:

1
2
3
4

openssl x509 -in ./google_com.pem -text -noout -certopt ca_default,no_validity,no_serial,no_subject,no_extensions,no_signame \
| grep -v 'Signature Algorithm' \
| tr -d '[:space:]:' \
| xxd -r -p > ./certificate-signature.bin

• openssl x509: extract the digital signature. openssl command supports certopt option, which allows multiple arguments separated by commas. The output of the first command should be:

1
2
3
4
5

Signature Algorithm: sha256WithRSAEncryption
        76:6a:8a:d8:44:ac:14:40:92:36:f3:4a:b5:cb:54:36:67:c7:
        <... content omitted ...>
        14:22:3f:2a:90:a5:e4:9b:26:df:33:15:4b:d2:5c:f7:89:8e:
        f7:6a:c4:a6

• grep -v: invert the sense of matching and select non-matching lines (because of -v option).Signature Algorithm: sha256WithRSAEncryption is matched, but only the Hex code lines are selected based on the invert-match rule. The data stream after filtering should be:

1
2
3
4

76:6a:8a:d8:44:ac:14:40:92:36:f3:4a:b5:cb:54:36:67:c7:
<... content omitted ...>
14:22:3f:2a:90:a5:e4:9b:26:df:33:15:4b:d2:5c:f7:89:8e:
f7:6a:c4:a6

Note Signature Algorithm: sha256WithRSAEncryption means that the signature is signed with SHA-256 hash function and RSA encryption algorithm. When we need to re-compute the hash again, we must use the same hash function: SHA-256.

• tr -d: delete the colons. The colons are to make it more readable. After removing the formatting colons, the output only contains Hex code.

• xxd -r -p: convert the Hex code into binary format and redirect to file certificate-signature.bin

Decrypt the signature

Now that we have both the digital signature and the public key of the intermediate CA. We can decrypt the signature as follows:

1

openssl rsautl -verify -inkey ./intermediate_ca_pub.pem -in ./certificate-signature.bin -pubin > ./certificate-signature-decrypted.bin

Store the decrypted signature in file certificate-signature-decrypted.bin. We can view the hash with openssl like so:

1

openssl asn1parse -inform der -in ./certificate-signature-decrypted.bin

The output is:

1
2
3
4
5

0:d=0  hl=2 l=  49 cons: SEQUENCE
2:d=1  hl=2 l=  13 cons: SEQUENCE
4:d=2  hl=2 l=   9 prim: OBJECT            :sha256
15:d=2  hl=2 l=   0 prim: NULL
17:d=1  hl=2 l=  32 prim: OCTET STRING      [HEX DUMP]:66EFBE4CEA76272C76CEE8FA297C1BF70C41F8E049C7E0E4D23C965CBE8F1B84

The hash is in the last line: 66EFBE4CEA76272C76CEE8FA297C1BF70C41F8E049C7E0E4D23C965CBE8F1B84.

Re-compute the hash

Now that we got the original hash of the certificate, we need to verify whether we can re-compute the same hash using the same hashing function (as mentioned above SHA-256 in this case).

The previous article explained that the digital signature is signed based on all of the information instead of only public key. We need to extract everything but the signature from the certificate.

We can extract the data and output it to file google_com_cert_body.bin as follows:

1

openssl asn1parse -i -in ./google_com.pem -strparse 4 -out ./google_com_cert_body.bin  -noout

Note: you can refer to this openssl document to have a deeper understanding about the behavior of this command.

Finally, let us re-compute the hash with SHA256 as follows:

1
2
3

openssl dgst -sha256 ./google_com_cert_body.bin

SHA256(./google_com_cert_body.bin)= 66efbe4cea76272c76cee8fa297c1bf70c41f8e049c7e0e4d23c965cbe8f1b84

The re-computed hash is 66efbe4cea76272c76cee8fa297c1bf70c41f8e049c7e0e4d23c965cbe8f1b84, which matches with the original hash. So we can get the conclusion that: the intermediate CA signs the goole.com server certificate.

Summary

In this article, we go through the verification process of SSL/TLS certificates step by step manually. I have to admit that the concepts of digital signatures and certificates are too abstract to understand, especially in the details. I hope the experiment, which carries out with certificates from the real world, can help you do that.

Reference

x509 Certificate Manual Signature Verification written by George Bolo.

Background

The second article of this series shows that we should not directly exchange public key to establish a secure channel. Instead, certificates should be used to establish trust between clients and servers. And the last article examines the content of certificates, which encodes two very crucial pieces of information: the server’s public key and a digital signature that can confirm the certificate’s authenticity. In this article, let us examine what digital signature is and how it works.

Digital Signature

The concept of digital signature can be illustrated as follows:

When the server sends a message to the client, how can we prevent the attackers from eavesdropping on the message? The solution is that the server attaches its signature to the message, and the client accepts the message only if the verification of the certificate passes. So this process can be divided into two parts: sign the message to get the digital signature and verify the digital signature.

• Sign the message: means hash the message and encrypt the hash with the server’s private key. The encrypted hash is called digital signature.

• Verify the signature: means decrypt the signature with the server’s public key to get the hash, re-compute the hash of the message again, and compare the identity of two hashes.

What can we benefit from signing and verifying the digital signature? To verify the digital signature is to confirm two things:

• Message Integrity: the message has not changed since the signature was attached because it is based on a cryptographic hash of the message.

• Proof of Origin: the signature belongs to the person who alone has access to the private key. In this way, the recipient of the message can be sure of the origin of the message.

Information security has other attributes, but integrity and authentication are the two traits you must know.

Secrets behind digital signature

As mentioned in the above section, the digital signature can prove the integrity of the message and the authenticity of the message’s owner. To understand how it works, you must understand the following two facts:

• Hash is irreversible

In the previous articles, we explained that cryptography is a two-way algorithm. You can encrypt the plaintext to the ciphertext and decrypt the ciphertext back to the plaintext. It means the cryptographic algorithm is reversible.

Different from cryptographic algorithms, A hash is irreversible!. This irreversibility is the whole point.

The goal of any cryptographic hashing algorithm is to reduce the arbitrarily sized input into a fixed-sized hash. The cryptographic hashing algorithm should guarantee that no two different messages can produce an identical hash. That is collide.

In this way, it is impossible for attackers to reverse engineer such a collision.

The attacker intercepts the message and changes it. Then the verification process of the signature on the client-side can not pass since the re-computed hashing can not match the original hashing.

I will write about how to implement a hash function in the future. In this article, you can ignore the details. Just remember that hashing is irreversible.

The private key prove identity

The attack shown above does not pass the verification because the signature and the forged message do not match. Then this time, the attacker compute a new hash based on the forged message and sign the hash with his private key. Can this attack work?

The short answer is No.

When the client gets the digital signature, the first step is to decrypt it. The decryption breaks for this new attack because the forged signature is signed with the attacker’s private key instead of the server’s private key.

It’s impossible for anybody except the owner of the private key to generate something that can be decrypted using the public key. This is the nature of public-key cryptography. I will write other articles to explain it mathematically in the future.

In a word, the private key can prove identity.

How does signature make certificate secure?

The digital signature is not designed only for TLS certificates, and it has other applications, which is not the focus of my article. The important thing is to understand how to apply digital signature in the PKI framework and how it makes certificates more secure.

The key is that the certificate associates the public key with the server you are connecting to. As we see in last article, the certificate must contain some information about the identity of the server, such as the domain name of the server. For example, the Subject property of the certificate we examined in the last article

1

Subject: CN = *.google.com

And the digital signature is signed based on all of the information instead of only public key. It can prevent man-in-the-middle attack in the two following cases:

• The attacker intercepts the server’s certificate and changes the public key or any other information, the hash code in the signature does not match the hash code of the content of the forged certificate, and the client rejects it. It is Message Integrity mentioned above.

• The attacker can obtain a certificate signed by the trusted CA by pretending as a legitimate business. When the client requests a certificate from the server, the attacker can replace it with his own. The validation on the client-side can not pass. Although the attacker’s certificate is signed by a trusted CA, the domain name(or other server information) does not match the expected one. It is Proof of Origin mentioned above.

So far, I hope you can understand (roughly) the beauty of this Internet security framework.

Summary

In this article, I examined how a digital signature works. You see how to sign a signature and how to verify it. Digital signature and certificate are the most abstract part of the PKI framework. So in the following article, let me illustrate the whole process by manually going through the certificate verification process step by step. We will use openssl to examine the result in each step.