Introduction
In this series of articles, I want to examine an important data structure: the red-black tree. The red-black tree is an advanced data structure that is difficult to fully understand. Maybe you have some wonders and confusion about it as follows:
- What is the meaning of
redandblackhere? - The
red-black treeis known as a self-balancing binary search tree. But what’s the difference between it and others? - Where is it used or applied?
If you want to know the answer to the above questions, then this article is just for you. I will cover the following topics:
- Why do we need the red-black tree and what is its advantage?
- How does a red-black tree work?
- How to write a red-black tree from scratch?
Background of Red-Black Tree
In this section, let’s review the history of the red-black tree. During this process, I will show you why it was invented and what kind of advantages it can provide compared with other tree data structures.
First thing first, let’s define the red-black tree as follows:
- Red-Black Tree is a
self-balancingbinarysearchtree.
Let’s analyze this definition step by step:
Tree: A tree is a
nonlineardata structure, compared toarrays,linked lists,stacksandqueueswhich arelineardata structures. A tree is a data structure consisting of one node called therootand zero or one or moresubtrees. One disadvantage oflineardata structures is the time required to search alinearlist is proportional to the size of the data set, which means that the time complexity isO(n). That’s why more efficient data structures like trees are invented tostoreandsearchdata.General Tree: A general tree is a tree where each node may have zero or more children.
Binary Tree: A binary tree is a specialized case of a general tree, where each node can have no more than
twochildren.Binary Search Tree: A binary tree satisfying the
binary searchproperty is called abinary search tree(BST). To build a BST, the node with a key greater than any particular node is stored on therightsub-trees and the one equal to or less than is stored on theleftsub-tree.
The average search time complexity of BST is O(logN), but in the worst case, it will be degraded to O(N). It happens when we insert the nodes one by one in order. For example, if we insert the elements in array [1, 2, 3, 4, 5, 6] into RST in order, what we get is as follows:
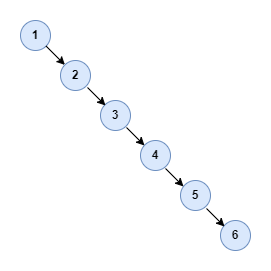
This kind of unbalanced BST is degraded to a single linked list. So the BST needs to keep balanced during the insert and delete of the node. That’s where the self-balancing binary search tree comes from.
- Self-Balancing Binary Search Tree: it’s a binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. And the red-black tree is just one type of it.
Summary
As the first post of this series, I examined the background of the red-black tree bit by bit. I hope you can understand what’s self-balancing binary search tree and why we need it. In the next post, I will start to examine the behavior and property of the red-black tree.