Deletion operation in Binary Search Tree: successor or predecessor

Introduction

Today, in this article I want to examine one concrete topic: how to delete a node from a binary search tree. This question is important for understanding other tree data structures, like the AVL tree, and the Red-Black tree.

As is common with many data structures, deletion is always the hardest operation. For example, to delete a specific element from the array, we need to shift all the elements after it by one index. And to delete one node from the linked list, we need to reset the pointer of the previous node (if it’s a doubled linked list, we need to reset more points, which is a more complex case). This is the same for the binary search tree as well. Let’s see in the following section.

Note: the idea of this article is inspired by the book Data Structures and Algorithm Analysis in C written by Mark Allen Weiss. The demo code shown in the following section is from this book. And I made some changes based on it. I highly recommend this great book to readers.

Deletion of the binary search tree

Before we can examine the deletion operation in depth, let’s quickly review the concept of the binary search tree as follows:

  • Binary search tree: is a binary tree holding the following property that for every node, X, in the tree, the values of all the keys in its left subtree are smaller than the key value in X, and the values of all the keys in its right subtree are larger than the key value in X.

Simply speaking, the binary search tree is a binary tree satisfying the binary search property. So each node of a binary search tree can have two children subtrees at most. When we need to delete one node from the binary search tree, then it’s necessary to consider the following 3 cases.

If the node is a leaf, then it can be deleted immediately. For example, to delete node 1 from the following binary search tree:

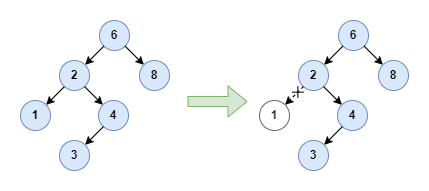
I will show you how to implement it at the code level later, which summarizes all the cases.

If the node has only one child subtree, the node can be deleted after we reset its parent’s pointer to bypass the node and point to its child node. For example, to delete node 4 as follows:

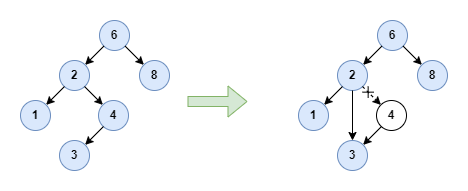
In the above example, node 4 has only one left child node 3. Let’s consider the symmetric scenario, imagine what will happen when it has only one right child node. The answer is it doesn’t influence how we handle the deleted node here and the result is the same. I will not draw the diagram here and leave it for you to explore.

The complicated case is how to deal with a node with two children. Before we introduce the solution, let’s clarify one concept about the binary search tree: successor:

  • Successor: is the node with the minimum value in the right subtree of any node.

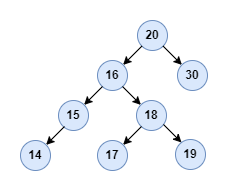
Let’s take node 16 in the above binary search tree as an example, the successor is node 17. All right! Based on this concept, the solution to delete a node with two children is straightforward:

  • Replace the data of the deleted node with the value of the successor and recursively delete the successor from the right subtree.

Let’s try to analyze this solution. Firstly, replacing the data of the node with the value of the successor can keep the binary search property after the deletion operation. Secondly, since the successor has the minimum value of the subtree, which means it cannot have a left child. So the successor is either a leaf node without any child node or a node with only one right child node. So recursively deleting the successor can be resolved by the two simple cases we discussed above, it’s perfect, right? For instance, the deletion of node 16 goes as follows:

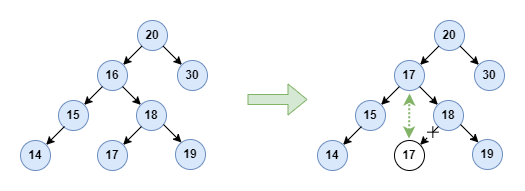
As we mentioned above, node 16‘s successor is node 17. So replace the value with 17 and delete node 17 from the right subtree, where node 17 is just a leaf node. Next, let’s implement the node deletion operation.

Code implementation

In this article, I will only show the codes related to the deletion operation rather than the complete implementation of a binary search tree. If you want to know how to write a BST from scratch, please refer to this GitHub repo.

Firstly, let’s examine the header file, which contains the data type definitions and function declarations. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include "utility.h"
#include <stdio.h>
#include <stdlib.h>

#ifndef _BST_H
#define _BST_H

typedef int ET;

struct TreeNode;
typedef struct TreeNode *Position;
typedef Position BST;

BST delete(ET, BST);
Position findMinBST(BST);

// code omitted here
#endif

You can notice that besides the delete function, we also define a helper function findMinBST which is used to find the successor node.

Next, let’s examine the function definitions as follows: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
BST
delete(ET elem, BST T)
{
    Position tmpCell;
  
    if (T == NULL)
        fatal("Element not found");
    else if (elem < T->Element)
        T->Left = delete(elem, T->Left);
    else if (elem > T->Element)
        T->Right = delete(elem, T->Right);
    else // we found the element to be deleted
    if (T->Left != NULL && T->Right != NULL) // two children
    {
        tmpCell = findMinBST(T->Right);
        T->Element = tmpCell->Element;
        T->Right = delete(T->Element, T->Right);
    }
    else // one or zero children, change the pointer T pointing to new address(NULl or the child node)
    {
        tmpCell = T;
        // for leaf node, T will be reset to null
        if (T->Right == NULL)
            T = T->Left;
        else if (T->Left == NULL)
            T = T->Right;
        free(tmpCell);
    }
    return T;
}

Position
findMinBST(BST T)
{
  if (T == NULL)
    return NULL;
  else if (T->Left == NULL)
    return T;
  else
    return findMinBST(T->Left);
}

I add some comments in the above code block which can help your understanding of this recursive algorithm. Please go ahead and think hard about it.

In the next section, we’ll have some open discussions about this solution. Let’s see whether there is any other solution. And what’re the potential issues of the current solution?

Open discussion

successor vs predecessor

Firstly, in the above solution, we delete the node with two children based on the successor. And there is the other concept called predecessor:

  • Predecessor: is the node with the maximum value in the left subtree of any node.

So similarly, the alternative solution to delete the node with two children is:

  • Replace the data of the deleted node with the value of the predecessor and recursively delete the predecessor from the left subtree.

We can do this by writing another helper function findMaxBST as follows: 

1
2
3
4
5
6
7
8
Position
findMaxBST(BST T)
{
  if (T != NULL)
    while (T->Right != NULL)
      T = T->Right;
  return T;
}

Does it work? The answer is yes. But the performance of the solution based on the predecessor is worse than the one based on the successor. Because the predecessor has the maximum value of the left subtree, it means that the predecessor can have two children. Then when we delete the predecessor recursively, the worst-case time complexity can reach O(logN) while the solution based on the successor only requires constant(O(1)) time. That’s the difference.

balanced vs unbalanced

Although the above solution can work, it exposes a serious performance issue. The reason why people invent binary search tree data structures is that we can get O(logN) level performance for searching operations. But imagine what will happen if we keep inserting and deleting nodes in the binary search tree in the way we mentioned here. The depth of the tree will become unbalanced. The left subtree grows deeper than the right subtree because we are always replacing a deleted node with the successor(which is from the right subtree, right?)

The following image is borrowed from Mark’s great book I mentioned above, which clearly shows that the tree becomes unbalanced after many rounds of insertion and deletion. If you want to know about it in theory, please refer to the book.

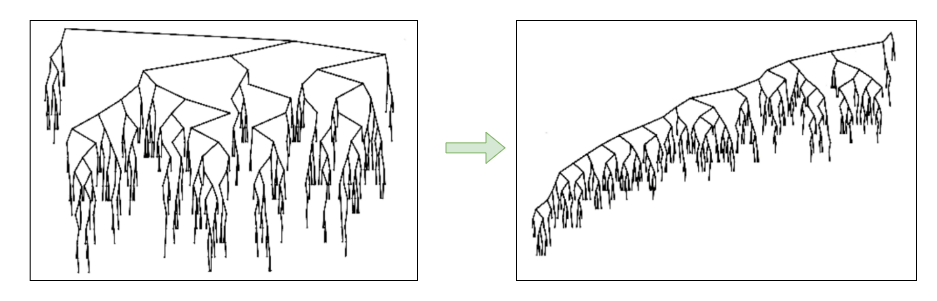
For an unbalanced BST, the worst-case time complexity can be degraded to O(n). To keep the desired performance, people invent a more advanced data structure self-balancing binary search tree, like the AVL tree and Red-black tree. I will share about them in the coming articles, please keep watching my blog.

Summary

In this article, we examined various solutions to delete a node from the binary search tree and evaluated their performance. We also discussed some open questions about BST, which prove why we need more advanced data structures like the red-black tree.