Background
In this article, I will focus on the topic of data structure and algorithms (in my eyes, one of the most important skills for software engineers). Someday I came across one question goes like this: how can building a heap be O(n) time complexity? This question confuses me for a while, so I did some investigation and research on it. This article will share what I learned during this process, which covers the following points:
- What is a heap data structure? How does a heap behave?
- How to implement a heap in C programming?
- How to do the time complexity analysis on building the heap?
Basics of Heap
Before we dive into the implementation and time complexity analysis, let’s first understand the heap.
As a data structure, the heap was created for the heapsort sorting algorithm long ago. Besides heapsort, heaps are used in many famous algorithms such as Dijkstra’s algorithm for finding the shortest path. Essentially, heaps are the data structure you want to use when you want to be able to access the maximum or minimum element very quickly.
In computer science, a heap is a specialized tree-based data structure. A common implementation of a heap is the binary heap, in which the tree is a binary tree.
So a heap can be defined as a binary tree, but with two additional properties (that’s why we said it is a specialized tree):
shape property: a binary heap is a complete binary tree. So what is a complete binary tree? That is all levels of the tree, except possibly the last one(deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right. The complete binary tree is one type of binary tree, in detail, you can refer to this document to learn more about it.
Heap property: the key stored in each node is either greater than or equal to (max-heaps) or less than or equal to (min-heaps) the keys in the node’s children.
The following image shows a binary max-heap based on tree representation:
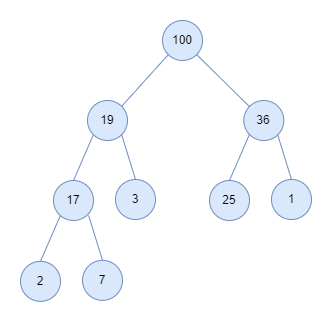
The heap is a powerful data structure; because you can insert an element and extract(remove) the smallest or largest element from a min-heap or max-heap with only O(log N) time. That’s why we said that if you want to access to the maximum or minimum element very quickly, you should turn to heaps. In the next section, I will examine how heaps work by implementing one in C programming.
Note: The heap is closely related to another data structure called the priority queue. The priority queue can be implemented in various ways, but the heap is one maximally efficient implementation and in fact, priority queues are often referred as “heaps”, regardless of how they may be implemented.
Implementation of Heap
Because of the shape property of heaps, we usually implement it as an array, as follows:
- Each element in the array represents a node of the heap.
- The parent/child relationship can be defined by the elements’ indices in the array. Given a node at index
i, the left child is at index2*i + 1and the right child is at index2*i + 2, and its parent is at index⌊(i-1)/2⌋(⌊⌋means Floor operation).
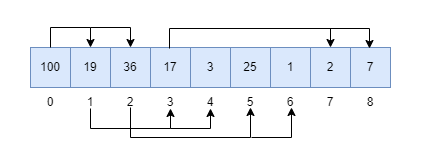
Based on the above model, let’s start implementing our heap. As we mentioned, there are two types of heaps: min-heap and max-heap, in this article, I will work on max-heap. The difference between max-heap and min-heap is trivial, you can try to write out the min-heap after you understand this article.
The completed code implementation is inside this Github repo.
First, let’s define the interfaces of max-heap in the header file as follows:
1 | // maxheap.h file |
We define the max-heap as struct _maxheap and hide its implementation in the header file. And expose this struct in the interfaces via a handler(which is a pointer) maxheap. This technique in C program is called opaque type. Opaque type simulates the encapsulation concept of OOP programming. So that the internal details of a type can change without the code that uses it having to change. The detailed implementation goes as following:
1 | // maxheap.c file |
The max-heap elements are stored inside the array field. The capacity of the array is defined as field max_size and the current number of elements in the array is cur_size.
Next, let’s go through the interfaces one by one (most of the interfaces are straightforward, so I will not explain too much about them). The first one is maxheap_create, which constructs an instance of maxheap by allocating memory for it.
1 | // maxheap.c file |
The initial capacity of the max-heap is set to 64, we can dynamically enlarge the capacity when more elements need to be inserted into the heap:
1 | // maxheap.c file |
This is an internal API, so we define it as a static function, which limits the access scope to its object file.
When the program doesn’t use the max-heap data anymore, we can destroy it as follows:
1 | // maxheap.c file |
Don’t forget to release the allocated memory by calling free.
Next, let’s work on the difficult but interesting part: insert an element in O(log N) time. The solution goes as follows:
- Add the element to the end of the array. (The end of the array corresponds to the leftmost open space of the bottom level of the tree).
- Compare the added element with its parent; if they are in the correct order(parent should be greater or equal to the child in max-heap, right?), stop.
- If not, swap the element with its parent and return to the above step until reaches the top of the tree(the top of the tree corresponds to the first element in the array).
The first step of adding an element to the array’s end conforms to the shape property first. Then the heap property is restored by traversing up the heap. The recursive traversing up and swapping process is called heapify-up. It is can be illustrated by the following pseudo-code:
1 | Max-Heapify-Up(A, i): |
The implementation goes as follows:
1 | // maxheap.c file |
The number of operations requried in heapify-up depends on how many levels the new element must rise to satisfy the heap property. So the worst-case time complexity should be the height of the binary heap, which is log N. And appending a new element to the end of the array can be done with constant time by using cur_size as the index. As a result, the total time complexity of the insert operation should be O(log N).
Similarly, next, let’s work on: extract the root from the heap while retaining the heap property in O(log N) time. The solution goes as follows:
- Replace the first element of the array with the element at the end. Then delete the last element.
- Compare the new root with its children; if they are in the correct order, stop.
- If not, swap the element with its child and repeat the above step.
This similar traversing down and swapping process is called heapify-down. heapify-down is a little more complex than heapify-up since the parent element needs to swap with the larger children in the max heap. The implementation goes as follows:
1 | // maxheap.c file |
Based on the analysis of heapify-up, similarly, the time complexity of extract is also O(log n).
In the next section, let’s go back to the question raised at the beginning of this article.
The time complexity of building a heap
What’s the time complexity of building a heap? The first answer that comes to my mind is O(n log n). Since the time complexity to insert an element is O(log n), for n elements the insert is repeated n times, so the time complexity is O(n log n). Right?
We can use another optimal solution to build a heap instead of inserting each element repeatedly. It goes as follows:
- Arbitrarily putting the n elements into the array to respect the shape property.
- Starting from the lowest level and moving upwards, sift the root of each subtree downward as in the
heapify-downprocess until the heap property is restored.
This process can be illustrated with the following image:
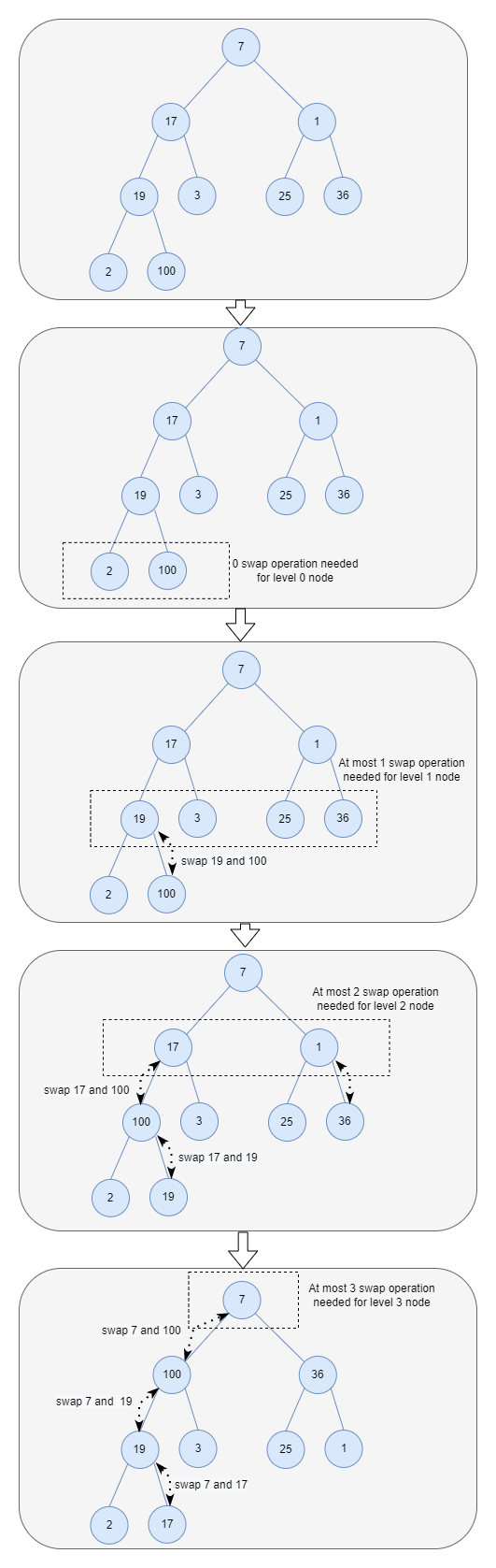
This algorithm can be implemented as follows:
1 | maxheap maxheap_heapify(const key_type* array, int n) { |
Next, let’s analyze the time complexity of this above process. Suppose there are n elements in the heap, and the height of the heap is h (for the heap in the above image, the height is 3). Then we should have the following relationship:
When there is only one node in the last level then . And when the last level of the tree is fully filled then
And start from the bottom as level 0 (the root node is level h), in level j, there are at most nodes. And each node at most takes j times swap operation. So in level j, the total number of operation is .
So the total running time for building the heap is proportional to:
If we factor out the term, then we get:
As we know, is a series converges to 2 (in detail, you can refer to this wiki).
Using this we have:
Based on the condition , so we have:
Now we prove that building a heap is a linear operation.
Summary
In this article, we examined what is a Heap and understand how it behaves(heapify-up and heapify-down) by implementing it. More importantly, we analyze the time complexity of building a heap and prove it’s a linear operation.